UNIV 1784: Mathematics, Political Representation, and Gerrymandering
Minn-Thu-Aye doing the math on a 24-foot-wide computer screen that is part of the Visualization Studio at Homer Babbidge Library.
Mathematics, Political Representation, and Gerrymandering (UNIV 1784)
Minn-Thu-Aye doing the math on a 24-foot-wide computer screen that is part of the Visualization Studio at Homer Babbidge Library.
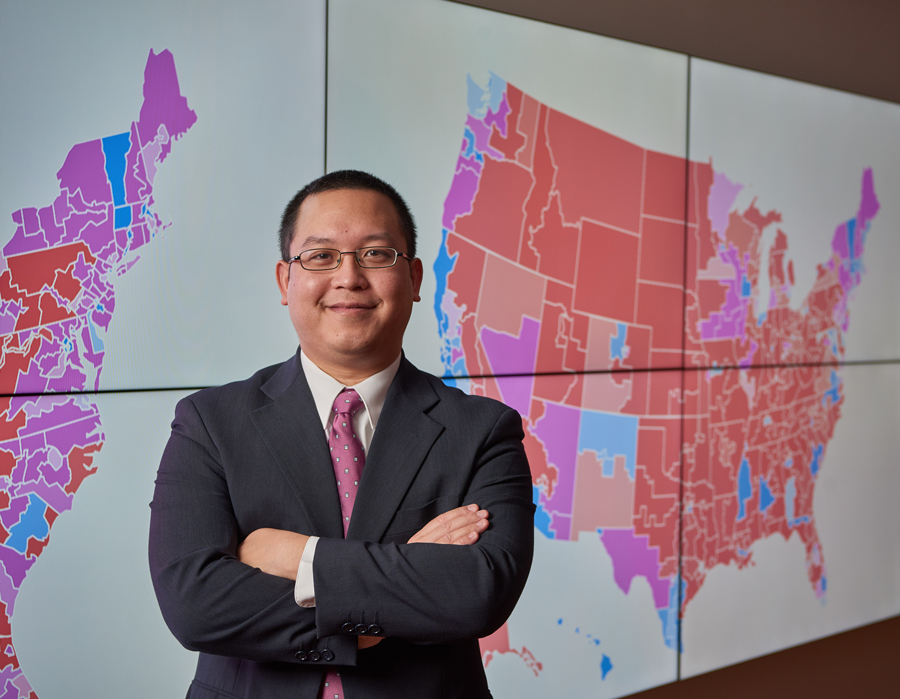
UNIV 1784 courses are freshman Honors courses that meet twice a week, once with faculty like Minn-Thu-Aye for academic forums and once with upperclass Honors students who prepare freshmen for the four-year Honors experience.
The Instructor:
Wearing jeans and a polo shirt, Myron Minn-Thu-Aye easily could be mistaken for an undergrad as he leads a post-mortem on the 2018 midterms. In truth, the boyish 33-year-old, an assistant professor-in-residence, has been following elections for as long as his students have been alive. His fascination can be traced to the American presidential campaign of 2000, when he was a student at a British high school in his native Hong Kong. "Florida was suddenly in the news," he says. "The Supreme Court was in the news. From far away it was something we talked about."
A few years after "hanging chad" briefly became a household term, Minn-Thu-Aye arrived in the U.S. as a freshman at Williams College. American elections were no longer distant events, and he remembers gathering with classmates to watch the returns as George Bush secured his second term in 2004. Meanwhile, his academic path was taking an unexpected turn.
"I had been good at math in school but had no intention of taking it any further," he says. "But all my dormmates seemed to be taking math classes, so I thought, sure, why not?" He enrolled in multivariable calculus his freshman year and was smitten. "Wow! This is something I need to explore more!" He ended up going straight from Williams to Louisiana State University, where he completed his Ph.D. in algebra in 2013.
Class Description:
A hot-button issue in recent years, the practice of gerrymandering — drawing electoral districts to manipulate the outcomes of elections — has been around almost as long as the Republic itself. It takes its name from Elbridge Gerry, signer of the Declaration of Independence and fifth vice president of the United States, who as Massachusetts governor in 1812 oversaw the creation of a Congressional district so sinuous it was said to resemble a salamander.
In "Mathematics, Representation, and Gerrymandering," Minn-Thu-Aye and his students apply the clear-eyed logic of data science to a bare-knuckle political practice, exploring the geometry of electoral districts and breaking down the relationship between redistricting and demographics.
"We're really looking for any kind of light that mathematics can shed on the electoral process and notions of fairness therein," says Minn-Thu-Aye. "We look at different types of data and learn about geometric and statistical ways to measure whether an election is meeting various criteria we might find desirable. A big goal is to add complexity to our views and understanding of elections."
Minn-Thu-Aye's Teaching Style:
On a morning not long after last fall's blue wave, the class is crunching numbers on ranked-choice voting (RCV), a type of balloting that allows voters to list multiple candidates by order of preference. Some experts believe that RCV can provide a more accurate measure of voters' wishes than the all-or-nothing system we commonly use.
The State of Maine implemented RCV for the midterms, and one result was that incumbent U.S. congressman Bruce Poliquin unexpectedly lost his seat. It was the first time in history that ranked choice had been used to decide a race for the U.S. Congress. Poliquin responded in the most American way possible: he filed a lawsuit.
After briefly noting that U.S. courts repeatedly have upheld the legitimacy of RCV (indeed, Poliquin's challenge would be summarily dismissed), Minn-Thu-Aye guides the class through an assessment of the various techniques used to slice and dice ranked-choice ballots. An instant runoff system, for example, takes the two candidates who garner the most first-place votes and eliminates everyone else. The top two are then tallied head to head, and the winner of that comparison wins the election. This is the system Maine used, but there are many others.
A time-tested method known as a Borda Count assigns point values to ballot positions — three points for every first-place vote, for instance, two points for second place, one point for third. Whoever racks up the most points wins. Outcomes can swing wildly depending on which method is used. Candidate A could win a Borda Count race without being anyone's first choice, while Candidate B might prevail over a crowded field in an instant runoff despite being dead last on a majority of ballots.
"How easily can techniques be manipulated?" Minn-Thu-Aye asks the class. "What conditions of fairness do we want our vote to satisfy?"
Why We Want to Take It Ourselves:
One year from now our country will embark on a Constitutionally mandated national census. Based on the data collected, electoral districts will be redrawn, Congressional representation will be reapportioned, and public funds will be redistributed to reflect population shifts. Meanwhile, the 2020 federal elections will put both the Senate and the White House in play. A proper understanding of these generation-defining events (the census and the presidential election coincide only once every 20 years) will require a sharp set of analytical tools.
"Math can surprise you," says Minn-Thu-Aye."It doesn't describe everything, it doesn't solve all your problems. But it captures some things very well. It can be a lens to look at these issues that I imagine are going to matter a lot to us, potentially on a personal level, in the quite near future."
—KEVIN MARKEY
UNIV 1784 courses are freshman Honors courses that meet twice a week, once with faculty like Minn-Thu-Aye for academic forums and once with upperclass Honors students who prepare freshmen for the four-year Honors experience.

Leave a Reply